七階四面體堆砌
在幾何學中,七階四面體堆砌是一種位於雙曲三維非緊空間的雙曲正堆砌,由正四面體組成,在施萊夫利符號中用{3,3,7}來表示,考克斯特-迪肯符號中以![]()
![]()
![]()
![]()
![]()
![]()
![]()
| 七階四面體堆砌 | |
|---|---|
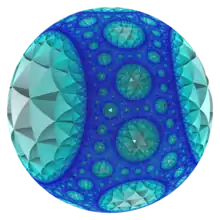 | |
| 類型 | 雙曲正堆砌 |
| 家族 | 堆砌 |
| 維度 | 三維雙曲空間 |
| 胞 | {3,3} |
| 面 | {3} |
| 顶点图 |  ({3,7}) |
| 施萊夫利符號 | {3,3,7} |
| 考克斯特記號 | |
| 對稱群 | [7,3,3] |
| 對偶多胞體 | 三階七邊形鑲嵌蜂巢體 |
| 特性 | 正 |
性質
由於正四面體不能堆滿三維空間,讓稜成為五個正四面體的公共稜之後,剩下的空間無法再放入一個正四面體,因此六階四面體堆砌就只能密鋪於雙曲空間[2],若再放入一個正四面體則無法存於雙曲緊湊空間,即圖形發散,無法收斂於無窮遠處。
相關多胞體與堆砌
七階四面體堆砌是一種由正四面體組成的堆砌,其他胞也由正四面體組成多胞體與堆砌或蜂巢體包含:
| {3,3,p}多胞體 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 空間 | S3 | H3 | |||||||||
| 構造 | 有限 | 仿緊 | 非緊 | ||||||||
| 施萊夫利符號 考克斯特符號 |
{3,3,3} |
{3,3,4} |
{3,3,5} |
{3,3,6} |
{3,3,7} |
{3,3,8} |
... {3,3,∞} | ||||
| 圖像 |  |
 |
 |
 |
 |
 |
 | ||||
| Vertex figure |
 {3,3} |
 {3,4} |
 {3,5} |
 {3,6} |
 {3,7} |
 {3,8} |
 {3,∞} | ||||
參見
參考文獻
- George Maxwell, Sphere Packings and Hyperbolic Reflection Groups, JOURNAL OF ALGEBRA 79,78-97 (1982) Archive.is的存檔,存档日期2013-06-30
- Hao Chen, Jean-Philippe Labbé, Lorentzian Coxeter groups and Boyd-Maxwell ball packings, (2013)页面存档备份,存于
- Humphreys, 1990, page 141, 6.9 List of hyperbolic Coxeter groups, figure 2 页面存档备份,存于
- The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN 0-486-40919-8 (Chapter 10, Regular Honeycombs in Hyperbolic Space 页面存档备份,存于)
- C. W. L. Garner, Regular Skew Polyhedra in Hyperbolic Three-Space Canad. J. Math. 19, 1179–1186, 1967. PDF 页面存档备份,存于
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.