五角化截半二十面體
在幾何學中,五角化截半二十面體是一種凸多面體,屬於康威多面體,有80個三角面,120個邊和42個頂點。乍看之下像是由正三角形組成,但實際上正三角形面只有二十个,其余的60个三角形面都是由等腰三角形所組成
| 五角化截半二十面體 | |
|---|---|
 (點選檢視旋轉模型) | |
| 類別 | 凸多面體 |
| 面 | 80 |
| 邊 | 120 |
| 頂點 | 42 |
| 歐拉特徵數 | F=80, E=120, V=42 (χ=2) |
| 頂點佈局 | (6) 35 (12) 36 |
| 康威表示法 | k4aC |
| 對稱群 | Ih群 |
| 對偶 | 截角菱形三十面體 |
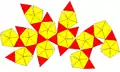 (展開圖) | |
參考文獻
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5
- Chapter 21: Naming the Archimedean and Catalan polyhedra and Tilings (p 284)
- Pentakis snub dodecahedron
- VTML polyhedral generator页面存档备份,存于 Try "k4aC" (康威多面體表示法)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.