多邊形二面體
多邊形二面體是由2個多邊形面組成的多面體,是一種二面體,是一種由兩個共用相同的一組邊的多邊形面組成的多面體。在三維歐幾里德空間中,如果它的面是平的,他們就會屬於退化的多面體,即與多邊形相同,定不具有體積;而在三維球面中,與平面的兩面體可以認為是透鏡,它的一個例子是一個透鏡空間的基本域。[1]
| 多邊形二面體 | |
|---|---|
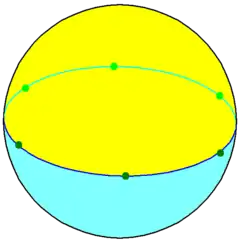 Example hexagonal dihedron on a sphere | |
| 類別 | 均勻多面體 or 球面鑲嵌 |
| 面 | 2 |
| 邊 | n |
| 頂點 | n |
| 歐拉特徵數 | F=2, E=n, V=n (χ=2) |
| 面的種類 | n邊形 |
| 考克斯特符號 | |
| 施萊夫利符號 | {n,2} |
| 威佐夫符號 | n 2 |
| 對稱群 | Dnh, [2,n], (*22n), order 4n |
| 對偶 | 多面形 |
| 旋轉對稱群 | Dn, [2,n]+, (22n), order 2n |
相關幾何圖形
| 圖像 |  |
 |
 |
 |
 |
| 施萊夫利 | {1,2} = h{2,2} | {2,2} | {3,2} | {4,2} | {5,2}... |
|---|---|---|---|---|---|
| 考克斯特 | |||||
| 面 | 2 {1} | 2 {2} | 2 {3} | 2 {4} | 2 {5} |
| 邊和 頂點 |
1 | 2 | 3 | 4 | 5 |
| 球面鑲嵌 | 二面體 | 歐式鑲嵌 仿緊空間 |
雙曲鑲嵌 非緊空間 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
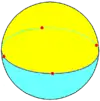
{1,2} |
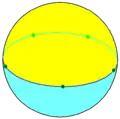
 {2,2} |
{3,2} |
 {4,2} |
{5,2} |
 {6,2} |
 {7,2} |
 {8,2} |
... |
 {∞,2} |
 {iπ/λ,2} |
參見
參考文獻
- Gausmann, Evelise; Roland Lehoucq, Jean-Pierre Luminet, Jean-Philippe Uzan, Jeffrey Weeks. . Classical and Quantum Gravity. 2001, 18: 5155–5186. arXiv:gr-qc/0106033. doi:10.1088/0264-9381/18/23/311.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.