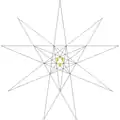
小三角六边形二十面体

在幾何學中，小三角六邊形二十面體是一種星形二十面體[1][2]，由20個等邊但不等角且互相相交的六邊形組成，其索引編號為DU₃₀。溫尼爾在他的書中列出28種星形多面體模型，並將小三角六邊形二十面體給予編號W₂₆[3]。其也收錄於哈羅德·斯科特·麥克唐納·考克斯特的書《五十九種二十面體》中，編號為2[4]。

小三角六邊形二十面體
小三角六邊形二十面體
類別	星形多面體
面	20
邊	60
頂點	32
歐拉特徵數	F=20, E=60, V=32 (χ=-8)
虧格	5
面的種類	20個等邊六邊形
頂點佈局	兩種頂點 5個六邊形的公共頂點 3個六邊形的公共頂點
對稱群	Ih, H3, [5,3], (*532)
參考索引	DU30, 2/59, W26
對偶	變數 "對偶多面體" 未定義。
特性	等面、等邊
變數 "對偶多面體" 未定義。 (對偶多面體)

小三角六邊形二十面體的對偶多面體是一種均勻多面體，是由五角星和三角形組成的小雙三斜三十二面體。

性質

小三角六邊形二十面體由20個面、60條邊和32個頂點組成[5][6]，每個面都是等邊六邊形，但不是正六邊形，每個六邊形彼此互相相交，其共存在兩種頂角，分別為5個六邊形的公共頂點和3個六邊形的公共頂點

作為星形多面體

作為一個星形多面體，其具有正二十面體的星狀核和五角化十二面體的凸包。

星狀圖	外觀	星狀核	凸包
		正二十面體	五角化十二面體

作為凹多面體

若作為凹多面體，即將原本互相相交的六邊形面去除隱沒部分其餘部分分為3個三角形，這種結構與星形三角化二十面體相同

星形三角化二十面體	小三角六邊形二十面體	三角化二十面體	正二十面體

頂點座標

小三角六邊形二十面體的頂點座標為[7]：

${\displaystyle (0,\pm {\frac {5-{\sqrt {5}}}{10}},\pm {\frac {5+{\sqrt {5}}}{10}})}$

${\displaystyle (\pm {\frac {5+{\sqrt {5}}}{10}},0,\pm {\frac {5-{\sqrt {5}}}{10}})}$

${\displaystyle (\pm {\frac {5-{\sqrt {5}}}{10}},\pm {\frac {5+{\sqrt {5}}}{10}},0)}$

${\displaystyle (\pm {\frac {3-{\sqrt {5}}}{2}},0,\pm {\frac {{\sqrt {5}}-1}{2}})}$

${\displaystyle (\pm {\frac {{\sqrt {5}}-1}{2}},\pm {\frac {3-{\sqrt {5}}}{2}},0)}$

${\displaystyle (0,\pm {\frac {{\sqrt {5}}-1}{2}},\pm {\frac {3-{\sqrt {5}}}{2}})}$

${\displaystyle (\pm {\frac {\sqrt {5}}{5}},\pm {\frac {\sqrt {5}}{5}},\pm {\frac {\sqrt {5}}{5}})}$

二面角

小三角六邊形二十面體二面角為負三分之一的反餘弦值[8]：

${\displaystyle \cos ^{-1}(-{\frac {1}{3}})\approx 1.9106\approx 109.4712^{\circ }}$

體積與表面積

一個邊長為a的小三角六邊形二十面體，其表面積和體積為[9]：

${\displaystyle A=3{\sqrt {15}}a^{2}\approx 11.61895a^{2}}$

${\displaystyle V={\frac {5+3{\sqrt {5}}}{4}}a^{3}\approx 2.92705a^{3}.}$

其中A代表表面積${\displaystyle A=3{\sqrt {15}}a^{2}}$約為11倍的邊長平方、V代表體積${\displaystyle V={\frac {1}{4}}(5+3{\sqrt {5}})a^{3}}$約為3倍的邊長立方。

相關多面體

對偶複合體

小三角六邊形二十面體與其對偶的複合體為複合小雙三斜三十二面體小三角六邊形二十面體。其共有52個面、120條邊和52個頂點，其尤拉示性數為-16，虧格為9，有12個非凸面，在威佐夫記號中以(3 | 5/2 3)表示[10]。

參考文獻

1. Wenninger, Magnus. . Cambridge University Press. 1974. ISBN 0-521-09859-9.
2. Wenninger, Magnus. . Cambridge University Press. 1983. ISBN 0-521-54325-8.
3. Coxeter, Harold Scott MacDonald; Du Val, P.; Flather, H. T.; Petrie, J. F. 3rd. Tarquin. 1999. ISBN 978-1-899618-32-3. MR676126. (1st Edn University of Toronto (1938))

1. . software3d.com. （原始内容存档于2015-09-21）.
2. Maeder, R. E. "The Stellated Icosahedra." Mathematica in Education 3, 5-11, 1994.
3. Wenninger, Magnus. . Cambridge University Press. 1974. ISBN 0-521-09859-9.
4. H·S·M·考克斯特. . H. T. Flather, J. F. Petrie. Springer Science & Business Media. 2012. ISBN 9781461382164.
5. . bulatov.org. （原始内容存档于2015-09-06）.
6. . craftsmanspace. （原始内容存档于2016-08-10）.
7. . dmccooey.com. （原始内容存档于2016-09-01）.
8. . dmccooey.com. （原始内容存档于2016-03-24）.
9. 埃里克·韦斯坦因. . MathWorld. （原始內容存檔於2016-08-01）.
10. . bulatov.org. （原始内容存档于2015-09-06）.

外部連結

• 埃里克·韦斯坦因. . MathWorld.
• 如何製作小三角六邊形二十面體 crafts4camp.com （英文）