希洛西七面體

希洛西七面體是非凸七面體的一種，拓撲結構的環，有7個凹六邊形面，每個面都與相鄰的面共用邊。因此，可用七種顏色來塗滿每個相鄰的面，是七色定理的下限。

希洛西七面體
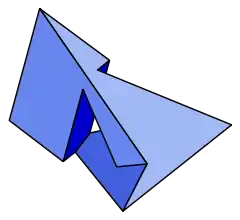(點選檢視旋轉模型)
類別	环形多面体
面	7
邊	21
頂點	14
歐拉特徵數	F=7, E=21, V=14 (χ=0)
虧格	1
面的種類	6個凹六邊形 1個凸六邊形
面的佈局	6.6.6
對稱群	Td, A3, [3,3], *332
對偶	恰薩爾十四面體
特性	凸、face-transitive
(展開圖)

性質

希洛西七面體是一個凹七面體，由7個面、21條邊和14個頂點組成。

它有一個180度的對稱軸；它有3對全等的面，和一個未成對六邊形面，也因此，該六邊形面具有跟整個多面體相同的旋轉對稱性。

希洛西七面體的14個頂點和21個邊形成了一個能嵌入環面表面的希伍德圖。

四面體和希洛西七面體是目前已知每個面都與其他面相鄰並共用邊的多面體。

面的組成

希洛西七面體由三組成對的凹六邊形面和一個不成對的凸六邊形面組成。

成對的面
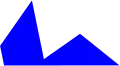不成對的面

頂角性質

希洛西七面體共有14個頂點，每個頂點對應的頂角都是由三個面組成的三面角。

頂點座標

若希洛西七面體的最短邊長為單位長，且幾何中心位於原點時，此時14頂點分別為:

${\displaystyle \left(-{\frac {24}{5}},0,{\frac {24}{5}}\right),}$

${\displaystyle \left(-{\frac {14}{5}},-1,{\frac {4}{5}}\right),}$

${\displaystyle \left(-{\frac {14}{5}},0,{\frac {4}{5}}\right),}$

${\displaystyle \left(-{\frac {9}{5}},1,{\frac {4}{5}}\right),}$

${\displaystyle \left(-{\frac {3}{2}},-{\frac {3}{2}},-{\frac {6}{5}}\right),}$

${\displaystyle \left(-{\frac {4}{5}},2,-{\frac {16}{5}}\right),}$

${\displaystyle \left(0,-{\frac {126}{25}},-{\frac {24}{5}}\right),}$

${\displaystyle \left(0,{\frac {126}{25}},-{\frac {24}{5}}\right),}$

${\displaystyle \left({\frac {4}{5}},-2,-{\frac {16}{5}}\right),}$

${\displaystyle \left({\frac {3}{2}},{\frac {3}{2}},-{\frac {6}{5}}\right),}$

${\displaystyle \left({\frac {9}{5}},-1,{\frac {4}{5}}\right),}$

${\displaystyle \left({\frac {14}{5}},0,{\frac {4}{5}}\right),}$

${\displaystyle \left({\frac {14}{5}},1,{\frac {4}{5}}\right),}$

${\displaystyle \left({\frac {24}{5}},0,{\frac {24}{5}}\right)}$

旋轉透視圖

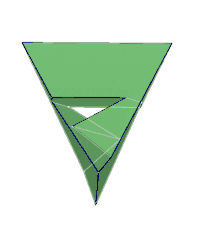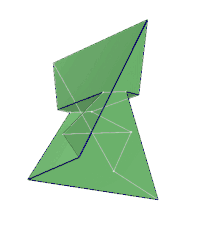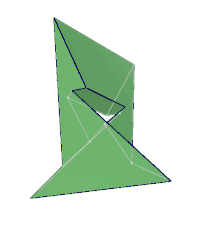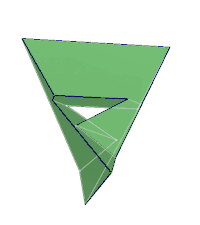參考文獻

• Császár, Ákos, , Acta Sci. Math. Szeged, 1949, 13: 140–142.
• Gardner, Martin, , Mathematical Games, Scientific American, 1978, 239 (5): 22–32, doi:10.1038/scientificamerican1178-22.
• Jungerman, M.; Ringel, Gerhard, , Acta Mathematica, 1980, 145 (1–2): 121–154, doi:10.1007/BF02414187.
• Peterson, Ivars, , , Mathematical Association of America, 2007, （原始内容存档于使用|archiveurl=需要含有|archivedate= (帮助)）.
• Szilassi, Lajos, (PDF), Structural Topology, 1986, 13: 69–80.
• Ace, Tom, , [2013-03-03], （原始内容存档于2016-09-07）.
• 埃里克·韦斯坦因. . MathWorld.
• Szilassi Polyhedron 页面存档备份，存于 - Papercraft model at CutOutFoldUp.com 页面存档备份，存于