平分線

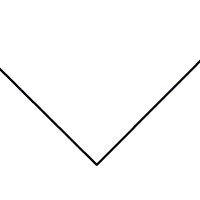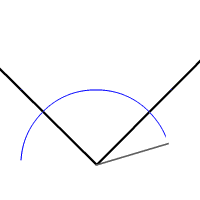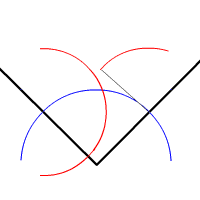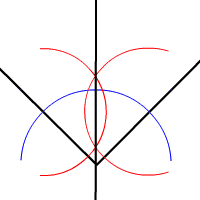
用直尺和圆规作出角平分线

平分線是一條能將一條線段二等分的線。

角平分線是將兩條線相交所夾的角二等分的線。

角平分线的性质

性质

角平分线是一条特殊的射线，它具有以下重要性质：

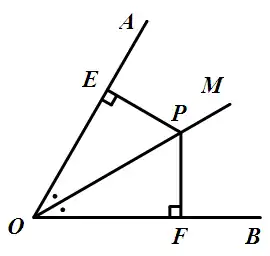
角平分线上的任意一点，到角两边的距离相等。

即如图所示：

${\displaystyle OM}$平分${\displaystyle {\angle }AOB,P}$为${\displaystyle OM}$上一点${\displaystyle ,PE{\perp }OA}$于${\displaystyle E,PF{\perp }OB}$于${\displaystyle F,}$

则${\displaystyle PE=PF.}$

该性质的证明

利用三角形全等，可以很容易推得此结论。

下面作一下简单推导。

${\displaystyle {\because \quad }OM}$平分${\displaystyle {\angle }AOB,}$

${\displaystyle {\therefore \quad \angle }POE={\angle }POF.}$

${\displaystyle {\because \quad }PE{\perp }OA,\;PF{\perp }OB,}$

${\displaystyle {\therefore \quad \angle }OEP={\angle }OFP=90^{\circ }.}$

在${\displaystyle {\triangle }OEP}$与${\displaystyle {\triangle }OFP}$中${\displaystyle ,}$

${\displaystyle {\begin{cases}{\angle }OEP={\angle }OFP,\\{\angle }POE={\angle }POF,\\OP=OP,\end{cases}}}$

${\displaystyle {\therefore \quad \triangle }OEP{\;\cong \triangle }OFP({\mbox{AAS}}).}$

${\displaystyle {\therefore \quad }PE=PF.}$

证毕。

角平分线的判定

判定

与其性质相对应的，就是角平分线的判定：

若有一點至角两边距离相等，則該點在該角的角平分线上。

即：

已知${\displaystyle {\angle }AOB,P}$为${\displaystyle OM}$上一点${\displaystyle ,\;PE{\perp }OA,\;PF{\perp }OB.}$

如果${\displaystyle PE=PF,}$那么${\displaystyle OM}$平分${\displaystyle {\angle }AOB.}$

证明

${\displaystyle {\because \quad }PE{\perp }OA,\;PF{\perp }OB,}$

${\displaystyle {\therefore \quad \angle }OEP={\angle }OFP=90^{\circ }.}$

在${\displaystyle \mathrm {Rt} {\triangle }OEP}$与${\displaystyle \mathrm {Rt} {\triangle }OFP}$中${\displaystyle ,}$

${\displaystyle {\begin{cases}OP=OP,\\PE=PF,\end{cases}}}$

${\displaystyle {\therefore \quad }\mathrm {Rt} {\triangle }OEP\;{\cong }\mathrm {Rt} {\triangle }OFP(\mathrm {HL} ).}$

${\displaystyle {\therefore \quad \angle }POE={\angle }POF,}$

${\displaystyle {\therefore \quad }OM}$平分${\displaystyle {\angle }AOB.}$

证毕。

內心

任意三角形ABC中，${\displaystyle {\angle }ABC}$、${\displaystyle {\angle }BCA}$、${\displaystyle {\angle }CAB}$ 角平分線交於一點I，則我們稱此點I為三角形ABC的內心。

三角形的內心恆在圖形內部，且到三角形之三邊距離等長

參見

• 角平分線長公式
• 垂直平分線
• 中线
• 高线