弦切角定理

弦切角定理（英語：）的定义是：交变段定理(也称为切弦定理)指出，在任何圆中，弦切角的度数等于通过一个弦和切线之间的端点的夹角，亦是所夹弧所对的圆周角（圆心角的一半）。

证明

已知：∠BAC是圆O的弦切角，AC与圆O相切，∠BAC所夹的弧是弧AB，∠APB是弧AB所对的圆周角.

求证：∠BAC=∠APB

证明：

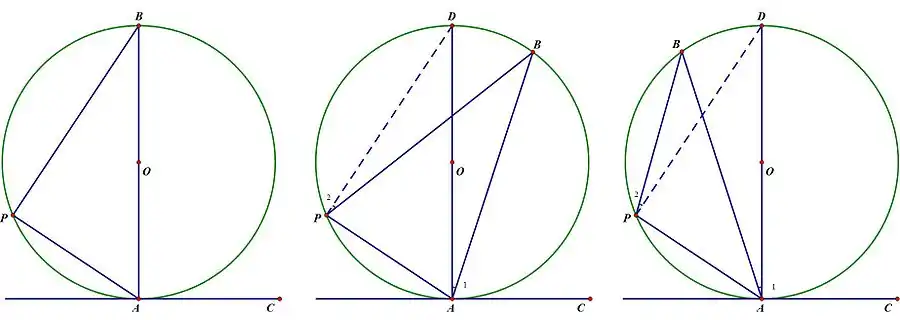
（1）当圆心O在∠BAC的弦AB上时，如图1.

∵AC与圆O相切於点A，AB是圆O的直径.

∴AB⊥AC

得∠BAC=90°

∵弧AB是半圆，∠APB是弧AB所对的圆周角.

∴∠APB=90°

∴∠BAC=∠APB

（2）当圆心O在∠BAC的外部时，如图2，作圆O的直径AD，再联结PD.

由（1）得∠DAC=∠APD

即∠1+∠BAC=∠2+∠APB

∵∠1=∠2

∴∠BAC=∠APB

（3）当圆心O在∠BAC的内部时，如图3，作圆O的直径AD，再联结PD.

由（1）得∠DAC=∠APD

即∠1+∠BAC=∠2+∠APD

∵∠1=∠2

∴∠BAC=∠APB

综上所述，总有∠BAC=∠APB.

参考文献

上海教育出版社 《数学》九年级拓展II