應變 (化學)

在化學的意義下，當一分子受到一應變影響，其化學結構對比於無應變的分子會受壓力而產生內能。所有的能量儲存於分子內的稱為內能。一受應變的分子相對於不受應變的分子有著額外的內能。這些額外的內能或稱為應變能，就如同壓縮的彈簧。[1]如同壓縮的彈簧一般，必須保持緊壓避免釋放出勢能，而分子可以不穩定的構型中維持內能是由於分子內的化學鍵，當這些化學鍵遭斷鍵則勢能就會瓦解。

摘要

熱力學

兩構象異構之間的化學平衡起因於兩構象不同能量的吉布斯能。因為能量的不同，則可以確定兩構象的平衡常數。

當一吉布斯能的能量下降從一狀態改變至另一狀態，則此轉變為自發反應，且在低能量下較為穩定。高能量分子會自發變成較低能量的構象。

例子:丁烷的對扭構象(anti)和間扭構象(gauche)

可透過吉布斯能方程式計算焓和熵(在常溫下)。

焓是一熱力學中重要的函數，常用來確定一更穩定的分子構象。[1]有多種不同的應變力，而這些應變能的產生在於分子內各種微弱的化學鍵。所以通常焓較為重要而熵通常都能省略。[1]但上述卻不是肯定的結果，當焓的值較小時則熵就不能省略。舉例來說，丁烷有兩種構象，對扭構象與間扭構象。對扭構象有較穩定的能量為0.9 kcal/mol。[1]則可以預期在室溫下丁烷會產生約82%的對扭構象和18%的間扭構象。但是間扭構象又有兩種可能，而對扭構象則直有一種可能。所以熵會在間扭構象中提供0.4 kcal的能量。[2]則可發現在實驗的結果式再室溫下產生70%的對扭構象和30%的間扭構象，證明在某些情況下熵是不能省略的。

確定分子的應變
環己烷和甲基環戊烷

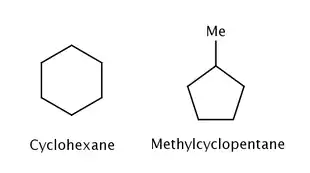
標準莫耳生成焓 (ΔHfo)指在標準狀態（101.3 kPa；25 ℃）下，生成1莫耳純淨物質放出（符號為負）或者吸收（符號為正）的熱量。[3]當化合物的生成熱和參考數據或是預測的不同，通常是受應變的影響。舉例來說，環己烷的生成熱 ΔHfo 為-29.9 kcal/mol而甲基環戊烷的生成熱 ΔHfo 為-25.5 kcal/mol。[1]環己烷和甲基環戊烷有著一樣的分子式和鍵數，但兩者的生成熱確存在著差異，是受到環張力的影響。在有關能量的實驗上，通常會使用燃燒熱，是一個較好設計使用且容易呈現的方式。

要先計算出應變能需要了解化合物在無受應變情況下的能量狀況。有兩種方式確定。 第一種，可以利用比較其他類似化合物且不受應變影響的分子，如同前面甲基環戊烷的例子，但通常要尋找到合適的化合物是困難的。第二種方式是利用Benson group increment theory，只需要利用增加或延長化合物放的分子(如接上新的烷基或是利用取代改變接的分子)，就能透過差異找出生成熱。而這些差距都是因為應變能的不同。

應變能的類型

凡得瓦張力

凡得瓦張力，或稱為立體張力，是未鍵結的原子彼此吸引靠近，而產生比凡得瓦半徑更為接近的構型。具體而言，凡得瓦張力是一種形式應變，互相作用的分子之間彼此距離四個鍵。[4]分子團的大小是影響立體張力的因素，體積龐大的叔丁基相較於甲基有著更大的空間可以進行空間交互作用。

Brown 等人研究關於三烷基胺和三甲機硼有關於立體張力的研究。[5] 他們發現增加三烷基胺的烷基鏈則平衡常數就會下降，利用三烷基胺和三甲基硼之間甲基團的立體張力去計算差異。

三烷基胺和三甲基硼的交互作用

順式-戊烷張力

在相似的構象下產生不同的應變能，這種情況下被稱為順式-戊烷張力。有兩種方式使戊烷的中心為間扭形式，第一種的能量高於其他構象 3 kcal/mol 的能量。[1] 當兩取代甲基從對扭變為間扭，則似環戊烷的構象兩端點的甲基就會互相接近。但如果兩端甲基轉至同一方向則此現象不會發生，兩終端的甲基團會受立體張力影響而被阻隔，兩種的構象有不同的能量差。


烯丙基張力
烯丙基甲基和乙基團相當靠近

烯丙基張力，或是 A1,3 張力和順式-戊烷張力是極為相似的。舉例來說，烯丙基的化合物中存在有 2-戊烯。而可以為乙基的烯烴取代基，而使的末端甲基靠近烯烴基團，鄰位的甲基就會旋轉。這種化合物需要較為線性的構象以避免取代基之間的。


1,3-二軸張力

1,3-二軸張力相似於順式-戊烷張力。因此張力的產生是介於環已烷環('α')的取代基和間扭構象的 alpha 取代基且兩者的亞甲基相隔兩個鍵遠。(是為1,3-二軸張力)。當取代基取代在軸向，會被帶靠近 gamma 位的氫。張力的大小受基團的大小影響，可以透過椅型結構下將取代基轉變為赤道向以緩解張力。構象之間的能量差被稱為A 值，由多種取代基構成。A 值是一個最早被測量出來可以用於吉布士方程的函數。

扭張力

扭張力是用來對抗鍵旋轉的張力。在環型結構的分子下，稱為皮策張力。

扭張力產生在當三鍵的原子處於重疊的形式下，能量不穩定，則產生扭張力。乙烷的交錯構象之間差2.9 kcal/mol的能量。[1]最初此旋轉障礙被判斷為和鄰位的氫的交互作用，但在這情況下氫的凡得瓦半徑太小了。最近的研究顯示交錯的構象更為穩定，因為超共軛效應的影響。[6]旋轉遠離可以中斷這種張力。

複雜的分子，如丁烷，可以有一種以上的交錯。對扭構象的丁烷的能量為3.8 kcal/mol 比間扭的丁烷更加穩定。[1]這些交錯的構象比重疊的構象穩定。受超共軛效應的影響，在丁烷中，受甲基團的空間交互作用影響和角張力產生反應。

環張力

根據價層電子對互斥理論中關於分子鍵結的部分，穩定的分子幾何形狀是鍵結的電子和非鍵結的電子要盡量遠離。為此在分子中會在角度上做一定程度上的壓縮和擴展以找到最好且穩定的角度。此張力被稱為角張力或是拜爾張力。[7]最簡單的角張力例子為小環烷烴類如環丙烷，環丁烷。下表顯示一些環烷類的應變能。


各種常見的環烷烴類的應變能[1]
環大小 應變能 (kcal/mol) 環大小 應變能 (kcal/mol)
3 27.5 10 12.4
4 26.3 11 11.3
5 6.2 12 4.1
6 0.1 13 5.2
7 6.2 14 1.9
8 9.7 15 1.9
9 12.6 16 2.0

原則上無環化合物是有機會出現角張力，但這現象是很罕見的。

小環烷烴類

環已烷被認定為確定環烷烴類有無張力的基準，被普遍的認為其應變能小到接近沒有。[1]一般而言，小環類的環烷烴有較大的應變能。環丙烷類似於三角形，其鍵角為 60 °C，遠低於109.5 °C 的sp3下的最穩定角度。此外環丙烷的氫為重疊的構象。環丁烷也有類似的應變能，其鍵角約為 88 °C和接近重疊的構象。環丙烷和環丁烷的應變能分別為27.5 和 26.3 kcal/mol。[1]環戊烷受張力較少，由重疊的氫扭轉使應變能降低，應變能為 6.2 kcal/mol。

跨環張力

令人訝異的是，中小型環(7-13環)比環己烷受到更大的張力影響。當跨環張力發生時，環烷烴類會極力避免角張力和扭張力的產生。為此，CH2 units會被互相帶靠近產生凡得瓦張力。


雙環系統

雙環系統中的應變能通常為各環應變能的總合，但有時要加入一些誘發產生的額外張力。

引用
  1. Anslyn and Dougherty, Modern Physical Organic Chemistry, University Science Books, 2006, ISBN 978-1-891389-31-3
  2. Coxon and Norman, Principles of Organic Synthesis, 3rd ed., Blackie Academic & Pro., 1993, ISBN 978-0-7514-0126-4
  3. Levine, Physical Chemistry, 5th ed., McGraw-Hill, 2002, ISBN 978-0-07-253495-5
  4. Brown, Foote, and Iverson, Organic Chemistry, 4th ed., Brooks/Cole, 2005, ISBN 978-0-534-46773-9
  5. Brown, H.C.; Johannesen, R.B. . J. Am. Chem. Soc. 1952, 75: 16–20. doi:10.1021/ja01097a005.
  6. Weinhold, F. . Nature. 2001, 411 (6837): 539–541. PMID 11385553. doi:10.1038/35079225.
  7. Wiberg, K. . Angew. Chem. Int. Ed. Engl. 1986, 25 (4): 312–322. doi:10.1002/anie.198603121.

參見
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.