截半黑塞二十七面體

在幾何學中，截半黑塞二十七面體是一個複正多面體，其位於${\displaystyle \mathbb {C} ^{3}}$複希爾伯特空間中由54個莫比烏斯－坎特八邊形組成，共有54個面、216條邊和72個頂點。其梵奧斯多邊形為施萊夫利符號計為₃{4}₃的二十四邊形、頂點圖為施萊夫利符號計為₃{4}₂的六邊形、對偶多面體為雙黑塞二十七面體。[2]

截半黑塞二十七面體
投影到實二維空間的平行投影
類別	複正多面體
面	54 3{3}3
邊	216 3{}
頂點	72
歐拉特徵數	F=54, E=216, V=72 (χ=-90)
皮特里多边形	十八边形
梵奧斯截面	9 3{4}3
面的種類	莫比烏斯－坎特八邊形
頂點圖	3{4}2
考克斯特符號	、.
施萊夫利符號	3{3}3{4}2
對稱群	M3 = 3[3]3[4]2, order 1296 3[3]3[3]3, order 648
對偶	雙黑塞二十七面體
特性	正

考克斯特指出，三個複正多面體黑塞二十七面體（）、雙黑塞二十七面體（，此多面體的對偶多面體）和截半黑塞二十七面體（）可以視為實空間多面體正四面體（）、立方體（）和正八面體（）在複空間的類比。[3]

截半黑塞二十七面體是一種位於複數空間的立體，其對應到實數空間同樣也有一種實數空間的代表，其為1₂₂多胞體，考克斯特表示法計為。[2]

性質

截半黑塞二十七面體位於${\displaystyle \mathbb {C} ^{3}}$複數空間中，由54個面、216條邊和72個頂點所組成。其中54個面為全等的莫比烏斯－坎特八邊形、216條邊皆為連接了三個頂點的稜，稱為三元稜或三元邊（Trion）[註 1]，在施萊夫利符號中可以用₃{}來表示[4]、72個頂點皆為6個莫比烏斯－坎特八邊形的公共頂點，在頂點圖中，這種頂點可以用施萊夫利符號計為₃{4}₂的六邊形表示；而其對多面體為由施萊夫利符號計為₃{4}₂的六邊形組成的七十二面體，稱為雙黑塞二十七面體。[5]

截半黑塞二十七面體可以視為黑塞二十七面體經過截半變換的結果，在截半的過程中，會產生形狀與原像的頂點圖相同、數量為原像頂點各數的面，[6]因此，黑塞二十七面體在經過截半變換後，產生了27個莫比烏斯－坎特八邊形的面，因此截半黑塞二十七面體共有54個面。[7]

面的組成

截半黑塞二十七面體由54個全等的莫比烏斯－坎特八邊形組成[8]。莫比烏斯－坎特八邊形是一種由8個頂點和8條稜所組成的幾何結構，其在施萊夫利符號中可以用₃{3}₃來表示、在考克斯特記號中可以用來表示。與一般的八邊形不同，莫比烏斯－坎特八邊形位於複希爾伯特平面，且構成這種形狀的稜每個稜階連接了三個頂點，稱為三元稜或三元邊（Trion），這種幾何結構在施萊夫利符號中可以用₃{}來表示。[4]

或由72個頂點、216條三元稜（或三元邊）和54 個3{3}3面組成

的其中一個3{3}3 面以藍色標示

的其中一個3{4}3形狀之梵奧斯多邊形以藍色標示

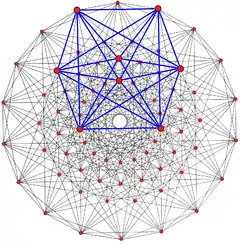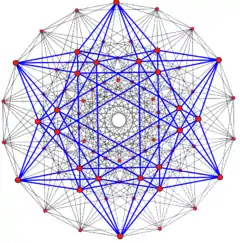結構

截半黑塞二十七面體的元素在布局矩陣中可以表示為正和擬正兩種形式[9]

M₃ = ₃[3]₃[4]₂對稱性

M3		k維面	fk	f0	f1	f2	k維頂點圖	備註
		( )	f0	72	9	6	3{4}2	M3/M2 = 1296/18 = 72
L1A1		3{ }	f1	3	216	2	{ }	M3/L1A1 = 1296/3/2 = 216
L2		3{3}3	f2	8	8	54	( )	M3/L2 = 1296/24 = 54

L₃ = ₃[3]₃[3]₃對稱性

L3		k維面	fk	f0	f1	f2		k維頂點圖	備註
L1L1		( )	f0	72	9	3	3	3{ }×3{ }	L3/L1L1 = 648/9 = 72
L1		3{ }	f1	3	216	1	1	{ }	L3/L1 = 648/3 = 216
L2		3{3}3	f2	8	8	27	*	( )	L3/L2 = 648/24 = 27
				8	8	*	27

對偶多面體

雙黑塞二十七面體
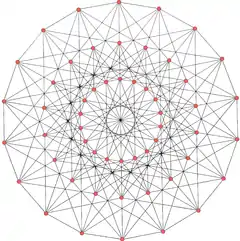投影到實二維空間的平行投影
類別	複正多面體
面	72個 2{4}3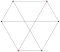
邊	216 { }
頂點	54
歐拉特徵數	F=72, E=216, V=54 (χ=-90)
皮特里多边形	十八边形
梵奧斯截面	{6}
面的種類	2{4}3
頂點圖	3{3}3
考克斯特符號
施萊夫利符號	2{4}3{3}3
對稱群	M3 = 3[3]3[4]2, order 1296
對偶	截半黑塞二十七面體
特性	正

截半黑塞二十七面體的對偶多面體又稱為雙黑塞二十七面體是一個位於${\displaystyle \mathbb {C} ^{3}}$複希爾伯特空間中由72個施萊夫利符號計為₂{4}₃的複多邊形組成，共有72個面、216條邊和54個頂點[5]，其可以經由黑塞二十七面體透過交錯變換構造而成，在考克斯特記號中可以用或表示，並與等價。

面的組成

雙黑塞二十七面體由72個全等且施萊夫利符號計為₂{4}₃的複多邊形組成[8]。這種多邊形位於${\displaystyle \mathbb {C} ^{2}}$複希爾伯特空間中由6個頂點和9條邊組成，在圖論中對應結構稱為湯瑪森圖[10]或4-cage[11]。

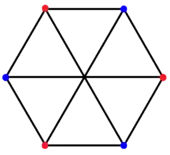雙黑塞二十七面體的面是一個2{4}3多邊形。圖中將其6個頂點著上紅色和藍色，並由9條二元邊相接形成完全二分图。

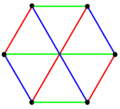其邊可分為三組，以不同顏色表示。

結構

雙黑塞二十七面體中的元素可以透過布局矩陣表示：

M3		k維面	fk	f0	f1	f2	k頂點	說明
L2		( )	f0	54	8	8	3{3}3	M3/L2 = 1296/24 = 54
L1A1		{ }	f1	2	216	3	3{ }	M3/L1A1 = 1296/6 = 216
M2		2{4}3	f2	6	9	72	( )	M3/M2 = 1296/18 = 72

正交投影

正交投影

多面體

多面體的其中一面以藍色表示。

多面體中52個頂點交替塗上兩種顏色。

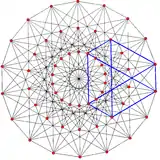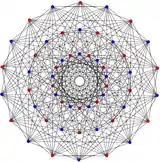在正複合立體中以紅色和藍色的頂點呈現與多面體。

註釋

1. 在數學中，邊或稜通常可以代表頂點皆只位在單一軸上並不涉及其他軸分量組成的幾何結構，例如x軸上的(2,0)連接到(3,0)的棱，但若將每一個維度從實數推廣至複數，則「軸」的概念可以被替換為高斯平面，這意味著稜不再只是一條線段，而可能是高斯平面上的一個區域。而三元邊或三元棱則為連接三個頂點所構成複數空間的棱。這種結構無法存於實空間，在實空間中，三元棱對應的幾何結構為三角形。

參考文獻

1. Coxeter, H. S. M., Moser, W. O. J.; Generators and Relations for Discrete Groups (1965), esp pp 67–80.
2. Coxeter, H. S. M.; Regular Complex Polytopes, Cambridge University Press, (1974).
3. Coxeter, H. S. M., Shephard, G.C.; Portraits of a family of complex polytopes, Leonardo Vol 25, No 3/4, (1992), pp 239–244,

1. Coxeter, H.S.M., , Cambridge University Press, 1991, ISBN 0-521-39490-2
2. Coxeter, 1991,[1] p.30, 47
3. Coxeter, 1991,[1] p.127
4. Coxeter, Complex Regular Polytopes,[1] 11.1 Regular complex polygons p.103
5. Coxeter, Regular Convex Polytopes, 1991,[1] p.30, 47
6. Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 (pp. 145–154 Chapter 8: Truncation)
7. Duke, Andrew Cameron, , Northeastern University, 2014
8. Stacey, Blake C, , sunclipse, December 30, 2018
9. Coxeter, Regular Convex Polytopes, 1991,[1] p.132
10. Coxeter, H. S. M., , Bulletin of the American Mathematical Society, 1950, 56: 413–455, MR 0038078, doi:10.1090/S0002-9904-1950-09407-5.
11. Coxeter, 1991,[1] p.110, 114