朗道分布

在概率论中,朗道分布（Landau distribution）[1]是因物理学家朗道而得名的一种概率分布。由于它所具有的长尾现象，这种分布的各阶矩（如数学期望与方差）都是未定义的。这种分布是稳定分布的一个特例。

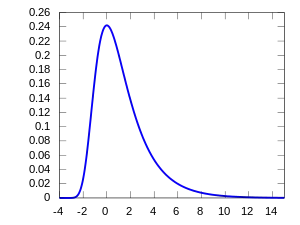
Landau distribution with mode at 2

定义

标准朗道分布的概率密度函数由以下复积分式表示，

${\displaystyle p(x)={\frac {1}{2\pi i}}\int _{c-i\infty }^{c+i\infty }\!e^{s\log s+xs}\,ds,}$

其中c为任意正实数，log以e为底，即取自然对数。上式结果不随c的改变而改变。为方便数值计算，可采用以下等价形式的积分式，

${\displaystyle p(x)={\frac {1}{\pi }}\int _{0}^{\infty }\!e^{-t\log t-xt}\sin(\pi t)\,dt,}$

通过将标准朗道分布扩展到一个位置-尺度分布族，就可以获得完整的朗道分布族。这种分布可以近似表示如下[2][3]，

${\displaystyle p(x)={\frac {1}{\sqrt {2\pi }}}\exp \left\{-{\frac {1}{2}}(x+e^{-x})\right\},}$

这种分布是稳定分布当参数α = 1且β = 1时的特例。[4]

其特征函数可表示如下，

${\displaystyle \varphi (t;\mu ,c)=\exp \!{\Big [}\;it\mu -|c\,t|(1+{\tfrac {2i}{\pi }}\log(|t|)){\Big ]},}$

其中μ和c是实数。它产生了一个由μ控制移动、由c控制缩放的朗道分布。[5]

相关性质

• 若${\displaystyle X\sim {\textrm {Landau}}(\mu ,c)\,}$ 则 ${\displaystyle X+m\sim {\textrm {Landau}}(\mu +m,c)\,}$
• 朗道分布是一种稳定分布

参考文献

1. Landau, L. . J. Phys. (USSR). 1944, 8: 201.
2. Melissinos, A.C. .
3. . [14 April 2014]. （原始内容存档于2012年6月30日）.
4. Gentle, James E. . Statistics and Computing 2nd. New York, NY: Springer. 2003: 196. ISBN 978-0-387-00178-4. doi:10.1007/b97336.
5. Meroli, S. . JINST. 2011, 6: 6013.