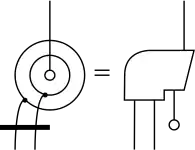
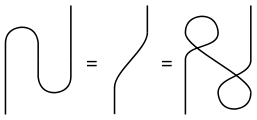潘洛斯圖形符號

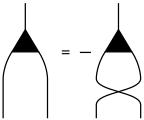
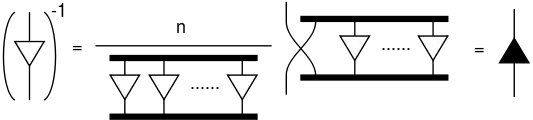
數學與物理學中，潘洛斯圖形符號（英語：）或稱張量圖符號（）是多線性函數或張量的一種圖形表示法，由羅傑·潘洛斯所提出。[1]

這樣的圖有多種幾何圖案，之間由線段相連。Predrag Cvitanović曾深入研究此方法，將之用在古典李群的分類上。[2]

透過表示論，此方法也被推廣至物理學中的自旋網路，以及線性代數中矩陣群相關的跡數圖。

詮釋

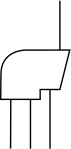
矩陣

特殊張量表象

度規張量

度規張量由U形或倒U形的迴圈所表示，正U或倒U由張量類型決定。

度規張量${\displaystyle g^{ab}\,}$

度規張量${\displaystyle g_{ab}\,}$

列維-奇維塔張量

列維-奇維塔反對稱張量由粗的水平橫桿來表示，其上有朝上或朝下的小棍，由張量類型所決定。

${\displaystyle \varepsilon _{ab\ldots n}}$

${\displaystyle \epsilon ^{ab\ldots n}}$

${\displaystyle \varepsilon _{ab\ldots n}\,\epsilon ^{ab\ldots n}}$${\displaystyle =n!}$

結構常數

李代數的結構常數（${\displaystyle {\gamma _{ab}}^{c}}$）由一帶有一條朝上線、兩條朝下線的小三角形所表示。

結構常數${\displaystyle {\gamma _{\alpha \beta }}^{\chi }=-{\gamma _{\beta \alpha }}^{\chi }}$

張量運算

指標縮併

指標進行張量縮併可由指標線相連來表示。

克羅內克δ函數 ${\displaystyle \delta _{b}^{a}}$

點積 ${\displaystyle \beta _{a}\,\xi ^{a}}$

${\displaystyle g_{ab}\,g^{bc}=\delta _{a}^{c}=g^{cb}\,g_{ba}}$

對稱化

指標的對稱化由水平穿越指標線的粗鋸齒狀橫桿來表示。

對稱化 ${\displaystyle Q^{(ab\ldots n)}}$ （其中${\displaystyle {}_{Q^{ab}=Q^{[ab]}+Q^{(ab)}}}$）

反對稱化

指標的反對稱化是由水平穿越指標線的粗直線來表示。

反對稱化 ${\displaystyle E_{[ab\ldots n]}}$ （其中${\displaystyle {}_{E_{ab}=E_{[ab]}+E_{(ab)}}}$）

行列式

行列式透過指標的反對稱化而形成。

行列式${\displaystyle \det \mathbf {T} =\det \left(T_{\ b}^{a}\right)}$

逆矩陣${\displaystyle \mathbf {T} ^{-1}=\left(T_{\ b}^{a}\right)^{-1}}$

協變導數

協變導數（${\displaystyle \nabla }$）是由一圍繞待運算之張量的圓圈所表示，另有一條朝下的線連接圓圈表示導數的下標。

協變導數${\displaystyle 12\nabla _{a}\left\{\xi ^{f}\,\lambda _{fb[c}^{(d}\,D_{gh]}^{e)b}\right\}}$

張量操作

圖形符號法在張量代數的操作中頗有用處。這些操作通常牽涉到一些與張量有關的恆等式。

舉例來說，一個常見的恆等式：

${\displaystyle \varepsilon _{a...c}\epsilon ^{a...c}=n!}$，

其中n是維度。

黎曼曲率張量

使用黎曼曲率張量所描述的里奇恆等式與比安基恆等式，可展示出潘洛斯圖形符號的威力。

黎曼曲率張量的符號

里奇張量 ${\displaystyle R_{ab}=R_{acb}^{\ \ \ c}}$

里奇恆等式${\displaystyle (\nabla _{a}\,\nabla _{b}-\nabla _{b}\,\nabla _{a})\,\mathbf {\xi } ^{d}}$${\displaystyle =R_{abc}^{\ \ \ d}\,\mathbf {\xi } ^{c}}$

比安基恆等式${\displaystyle \nabla _{[a}R_{bc]d}^{\ \ \ e}=0}$

擴充

此符號標記法已擴充到旋量與扭量的使用。[3][4]

相關條目

• 抽象指標記號
• 里奇微積分
• 自旋網路
• 角動量圖

參考文獻

1. see e.g. Quantum invariants of knots and 3-manifolds" by V. G. Turaev (1994), page 71
2. Predrag Cvitanović. . Princeton University Press. 2008 [2015-05-23]. （原始内容存档于2011-07-20）.
3. Penrose, R.; Rindler, W. . Cambridge University Press. 1984: 424–434. ISBN 0-521-24527-3.
4. Penrose, R.; Rindler, W. . Cambridge University Press. 1986. ISBN 0-521-25267-9.

外部連結