狄利克雷分布

狄利克雷分布是一组连续多变量概率分布，是多变量普遍化的Β分布。为了纪念德国数学家約翰·彼得·古斯塔夫·勒熱納·狄利克雷（Peter Gustav Lejeune Dirichlet）而命名。狄利克雷分布常作为贝叶斯统计的先验概率。当狄利克雷分布维度趋向无限时，这过程便称为狄利克雷过程（Dirichlet process）。

狄利克雷分布

密度函數
	${\displaystyle K\geq 2}$ 分类数 (整数) ${\displaystyle \alpha _{1},\ldots ,\alpha _{K}}$ concentration parameters，${\displaystyle \alpha _{i}>0}$
值域	${\displaystyle x_{1},\ldots ,x_{K}}$，${\displaystyle x_{i}\in (0,1)}$，${\displaystyle \sum _{i=1}^{K}x_{i}=1}$
	${\displaystyle {\frac {1}{\mathrm {B} ({\boldsymbol {\alpha }})}}\prod _{i=1}^{K}x_{i}^{\alpha _{i}-1}}$ ${\displaystyle \mathrm {B} ({\boldsymbol {\alpha }})={\frac {\prod _{i=1}^{K}\Gamma (\alpha _{i})}{\Gamma {\bigl (}\sum _{i=1}^{K}\alpha _{i}{\bigr )}}}}$ ${\displaystyle {\boldsymbol {\alpha }}=(\alpha _{1},\ldots ,\alpha _{K})}$
期望值	${\displaystyle \operatorname {E} [X_{i}]={\frac {\alpha _{i}}{\sum _{k}\alpha _{k}}}}$ ${\displaystyle \operatorname {E} [\ln X_{i}]=\psi (\alpha _{i})-\psi (\textstyle \sum _{k}\alpha _{k})}$ (试看 digamma function)
眾數	${\displaystyle x_{i}={\frac {\alpha _{i}-1}{\sum _{k=1}^{K}\alpha _{k}-K}},\quad \alpha _{i}>1.}$
	${\displaystyle \operatorname {Var} [X_{i}]={\frac {{\tilde {\alpha }}_{i}(1-{\tilde {\alpha }}_{i})}{{\bar {\alpha }}+1}},}$ 其中${\displaystyle {\tilde {\alpha }}_{i}={\frac {\alpha _{i}}{\sum _{i=1}^{K}\alpha _{i}}}}$ 而且${\displaystyle {\bar {\alpha }}=\sum _{i=1}^{K}\alpha _{i}}$ ${\displaystyle \operatorname {Cov} [X_{i},X_{j}]={\frac {-{\tilde {\alpha }}_{i}{\tilde {\alpha }}_{j}}{{\bar {\alpha }}+1}}~~(i\neq j)}$
熵	${\displaystyle H(X)=\log \mathrm {B} (\alpha )+(\alpha _{0}-K)\psi (\alpha _{0})-\sum _{j=1}^{K}(\alpha _{j}-1)\psi (\alpha _{j})}$
	{{{mgf}}}
特徵函数	{{{char}}}

狄利克雷分布奠定了狄利克雷过程的基础，被广泛应用于自然语言处理特别是主题模型（topic model）的研究。

概率密度函数

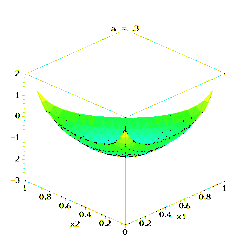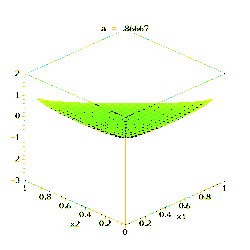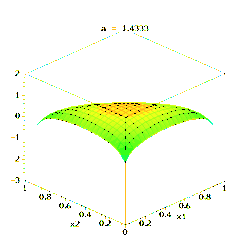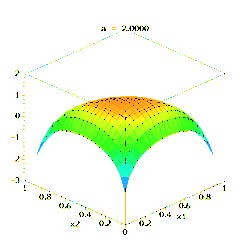
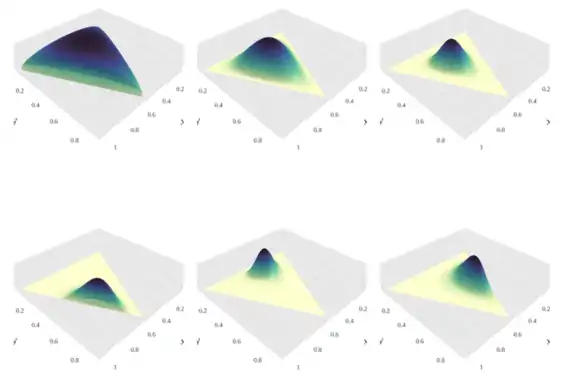
此图展示了当K=3、参数α从α=(0.3, 0.3, 0.3)变化到(2.0, 2.0, 2.0)时，密度函数取对数后的变化。

维度K ≥ 2的狄利克雷分布在参数α₁, ..., α_K > 0上、基于欧几里得空间R^K-1里的勒贝格测度有个概率密度函数，定义为：

${\displaystyle f(x_{1},\dots ,x_{K};\alpha _{1},\dots ,\alpha _{K})={\frac {1}{\mathrm {B} (\alpha )}}\prod _{i=1}^{K}x_{i}^{\alpha _{i}-1}}$

x₁, ..., x_K–1 > 0并且x₁ + ... + x_K–1 < 1，x_K = 1 – x₁ – ... – x_K–1. 在(K − 1)维的单纯形开集上密度为0。

归一化衡量B(α)是多项Β函数，可以用Γ函数（gamma function）表示：

${\displaystyle \mathrm {B} (\alpha )={\frac {\prod _{i=1}^{K}\Gamma (\alpha _{i})}{\Gamma {\bigl (}\sum _{i=1}^{K}\alpha _{i}{\bigr )}}},\qquad \alpha =(\alpha _{1},\dots ,\alpha _{K}).}$

参见

• 約翰·彼得·古斯塔夫·勒熱納·狄利克雷
• 狄利克雷过程
• 隐含狄利克雷分布

參考

• Introduction to the Dirichlet Distribution and Related Processes by Frigyik, Kapila and Gupta
• Dirichlet processes by Yee Whye Teh