罩帳
在幾何學中,又稱為,是指一系列屬於二面體群的多面體,正如其名「」,就如帳篷般的結構。罩帳是指有兩個在空間中平行的正多邊形,其中一個的邊數是另一個的兩倍。在兩者間加入三角形和正五邊形。罩帳與帳塔類似但不是正方形和三角形交替構成,而是五邊形和三角形交替並繞軸構成。罩帳的命名取決於邊數較少的一個面,最小的罩帳為三角罩帳,由六邊形的底面和三角形的頂面構成,二角罩帳也可以視為罩帳的一種,但其頂面已退化,但整體並未像二角錐或二角柱完全退化。若一個罩帳底面為正多邊形則可以稱為正罩帳,但側面未必能為正多邊形。所有面都是正多邊形的罩帳只有正五角罩帳。
| 罩帳 | |
|---|---|
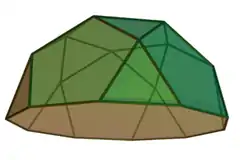 以五角罩帳為例 | |
| 類別 | 罩帳 |
| 面 | 3n + 2 |
| 邊 | 7n |
| 頂點 | 4n |
| 歐拉特徵數 | F=3n + 2, E=7n, V=4n (χ=2) |
| 面的種類 | 1個n邊形 1個2n邊形 n個五邊形 2n個三角形 |
| 對稱群 | Cnv, [n], (*nn), order 2n |
| 對偶 | 罩帳對偶 |
| 旋轉對稱群 | Cn, [n]+, (nn), order n |
| 特性 | 凸 |
 罩帳對偶 (對偶多面體) |
 (展開圖) |
所有罩帳只有一種屬於詹森多面體,即正五角罩帳。
參見
- 雙罩帳
- 詹森多面體
參考文獻
- Norman W. Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
- Victor A. Zalgaller. . Consultants Bureau. 1969. No ISBN. The first proof that there are only 92 Johnson solids.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.