西姆松定理

西姆松定理說明：有三角形${\displaystyle ABC}$，平面上有一點${\displaystyle P}$。${\displaystyle P}$在三角形三邊上的投影（即由${\displaystyle P}$到邊上的垂足）共線（此線稱為西姆松線或譯「西摩松線」, Simson line）若且唯若${\displaystyle P}$在三角形的外接圓上。

相關的結果有：

• 稱三角形的垂心為H。西姆松線和PH的交點為線段PH的中點，且這點在九點圓上。
• 兩點的西姆松線的交角等於該兩點的圓周角。
• 若兩個三角形的外接圓相同，這外接圓上的一點P對應兩者的西姆松線的交角，跟P的位置無關。

证明

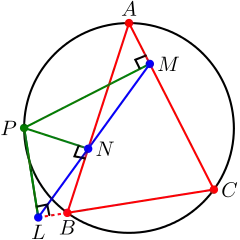
如图，若L、M、N三点共线，连结BP，CP，则因PL垂直于BC，PM垂直于AC，PN垂直于AB，有B、P、L、N和M、P、L、C分别四点共圆，有

角PBN = 角PLN = 角PLM = 角PCM

故A、B、P、C四点共圆。

若A、B、P、C四点共圆，则角PBN = 角PCM。因PL垂直于BC，PM垂直于AC，PN垂直于AB，有B、P、L、N和M、P、L、C四点共圆，有

角PLN = 角PBN = 角PCM = 角PLM

故L、M、N三点共线。

参见

• 九点圆

外部連結

• cut-the-knot網站上的證明
• 證明（flash）