三角反棱柱
在幾何學中，三角反棱柱是基底為三角形的反棱柱。其側面必為等腰三角形，但底面可以是任意三角形。所有三角反棱柱皆為八面體，具有8個面、12個邊和6個頂點。
| 三角反棱柱 | |
|---|---|
 | |
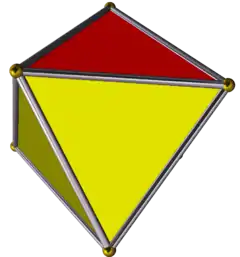| 類別 | 反棱柱 |
| 面 | 8 |
| 邊 | 12 |
| 頂點 | 6 |
| 歐拉特徵數 | F=8, E=12, V=6 (χ=2) |
| 面的種類 | 等腰三角形×6 任意三角形×2 |
| 面的佈局 | 6{3}+2{3} |
| 頂點圖 | 3.3.3.3 |
| 考克斯特符號 |      |
| 施萊夫利符號 | s{2,3} |
| 威佐夫符號 | | 2 2 3 |
| 康威表示法 | A3 |
| 對稱群 | D3d, [2+,6], (2*3), order 12 |
| 參考索引 | U77(a) |
| 對偶 | 三方偏方面體 |
| 旋轉對稱群 | D3, [3,2]+, (332), order 6 |
| 特性 | 凸 |
 三方偏方面體 (對偶多面體) | |
和其他反稜柱不同在於，正三角反棱柱在底面和側面皆為正三角形時是正多面體，即正八面體，而其它的正多角反棱柱只能算是一種半正多面體（或均勻多面體）。
正三角反棱柱
當底面為正三角形時，側面為等腰三角形未必為正三角形時，此時就可以稱為正三角反棱柱。在施萊夫例符號中用s{2,3}表示可以藉由三面形透過扭稜變換構造而來，而在考克斯特記號中以或表示，具有D3d, [2+,6], (2*3)對稱性和D3, [3,2]+, (332)旋轉對稱性。
若底面與側面皆為正三角形時，則該立體將與正八面體無異，在施莱夫利符号{3,4}表示，而在考克斯特符號中以
表示，具有比上述立體更高的對稱性Oh, BC3, [4,3], (*432)和O, [4,3]+, (432)旋轉對稱性。
其他反棱柱
相關多面體與鑲嵌
三角反棱柱可以由三角形二面體的對偶三面形透過扭稜變換構造而來，因此與三角形二面體具有相同的對稱性，其可以衍生出一些相關的多面體：
| 對稱群：[3,2], (*322) | [3,2]+, (322) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
 |
|
|
|
|
|
|
| ||
 |
 |
|
 |
 |
 |
 | |||
| {3,2} | t{3,2} | r{3,2} | 2t{3,2}=t{2,3} | 2r{3,2}={2,3} | rr{3,2} | tr{3,2} | sr{3,2} | ||
| 半正對偶 | |||||||||
 |
|
|
|
|
|
|
 | ||
|
 |
|
 |
|
|
 |
 | ||
| V32 | V62 | V32 | V4.4.3 | V23 | V4.4.3 | V4.4.6 | V3.3.3.3 | ||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | n |
|---|---|---|---|---|---|---|---|---|---|---|---|
| s{2,4} sr{2,2} |
s{2,6} sr{2,3} |
s{2,8} sr{2,4} |
s{2,10} sr{2,5} |
s{2,12} sr{2,6} |
s{2,14} sr{2,7} |
s{2,16} sr{2,8} |
s{2,18} sr{2,9} |
s{2,20} sr{2,10} |
s{2,22} sr{2,11} |
s{2,24} sr{2,12} |
s{2,2n} sr{2,n} |
|
|
 |
   |
|
 |
|
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| 作為球面鑲嵌 | |||||||||||
 |
|
 |
 |
 |
 |
 |
|||||
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.