内侧菱形三十面体

在幾何學中，內側菱形三十面體，又稱小星形三十面體[1][2]是一種菱形三十面體的星形多面體[3]，由30個全等且互相相交的菱形組成。其對偶多面體為截半大十二面體。

內側菱形三十面體
內側菱形三十面體
類別	星形多面體
面	30
邊	60
頂點	24
歐拉特徵數	F=30, E=60, V=24 (χ=-6)
面的種類	30個菱形
對稱群	Ih, [5,3], *532
參考索引	DU36
對偶	變數 "對偶多面體" 未定義。
特性	等面、非凸
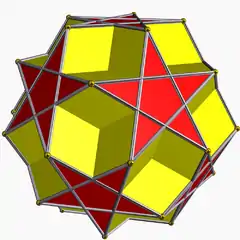變數 "對偶多面體" 未定義。 (對偶多面體)

性質

內側菱形三十面體由30個面、60條邊和24個頂點組成，其30個面皆由菱形組成。內側菱形三十面體有兩種頂角，一種由菱形的銳角組成，頂點圖為五邊形；另一種由菱形的鈍角組成，頂點圖為五角星，其中，頂點圖為五角星的頂點藏在圖形內部[4]。

頂點座標

對偶邊長為1的內側菱形三十面體的頂點座標為[5]：

${\displaystyle (\pm {\frac {3}{4}},0,\pm {\frac {3(1+{\sqrt {5}})}{8}})}$

${\displaystyle (\pm {\frac {3(1+{\sqrt {5}})}{8}},\pm {\frac {3}{4}},0)}$

${\displaystyle (0,\pm {\frac {3(1+{\sqrt {5}})}{8}},\pm {\frac {3}{4}})}$

${\displaystyle (\pm {\frac {3({\sqrt {5}}-1)}{8}},0,\pm {\frac {3}{4}})}$

${\displaystyle (\pm {\frac {3}{4}},\pm {\frac {3({\sqrt {5}}-1)}{8}},0)}$

${\displaystyle (0,\pm {\frac {3}{4}},\pm {\frac {3({\sqrt {5}}-1)}{8}})}$

二面角

大六角二十四面體僅有一種二面角，為兩個菱形的棱之交角，其值為負二分之一的反餘弦值[6]：

${\displaystyle \cos ^{-1}(-{\frac {1}{2}})={\frac {2\pi }{3}}\approx 2.0943=120^{\circ }}$

相關多面體

內側菱形三十面體在拓樸中相當於五階正方形鑲嵌的商空間，其可以將作為內側菱形三十面體中的菱形面進行拓樸變形成正方形而構造出五階正方形鑲嵌，因此在另外一個索引中也被看作是一種正多面體[7]：

其他四種抽象正多面體為：

多面體	內側菱形三十面體	十二合十二面體	內側三角星化二十面體	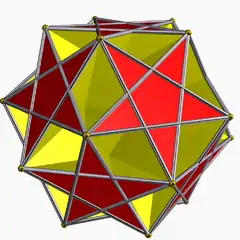雙三斜十二面體	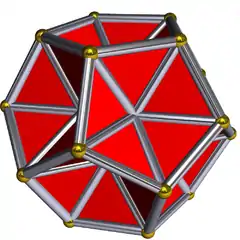凹五角錐十二面體
頂點圖	{5}, {5/2}	(5.5/2)^2	{5}, {5/2}	(5.5/3)^3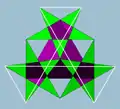
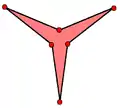面	30個菱形	12個五邊形 12個五角星	20個六邊形	12個五邊形 12個五角星	20個六邊形
鑲嵌	{4, 5}	{5, 4}	{6, 5}	{5, 6}	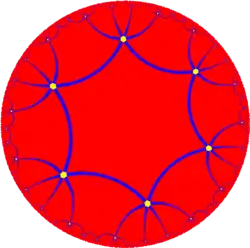{6, 6}
χ	−6	−6	−16	−16	−20

參考文獻

1. Wenninger, Magnus. . Cambridge University Press. 1974. ISBN 0-521-09859-9.
2. Wenninger, Magnus. . Cambridge University Press. 1983. ISBN 0-521-54325-8.
3. Coxeter, Harold Scott MacDonald; Du Val, P.; Flather, H. T.; Petrie, J. F. 3rd. Tarquin. 1999. ISBN 978-1-899618-32-3. MR676126. (1st Edn University of Toronto (1938))

1. Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, 1973. ISBN 978-0486614809 p. 102-103
2. 埃里克·韦斯坦因. . MathWorld. （原始內容於2016-09-01）.
3. . software3d.com. [2016-09-01]. （原始内容存档于2016-03-04）.
4. Wenninger, M. J. Dual Models. Cambridge, England: Cambridge University Press, pp. 41 and 46, 1983. ISBN 978-0521245241
5. . dmccooey.com. [2016-09-01]. （原始内容存档于2016-09-01）.
6. . dmccooey.com. [2016-09-01]. （原始内容存档于2016-03-24）.
7. David A. Richter. . 西密西根大學. [2013-05-05]. （原始内容存档于2016-03-04）.

外部連結

• 埃里克·韦斯坦因. . MathWorld.