凹五角錐十二面體

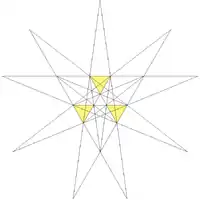
在幾何學中，凹五角錐十二面體是一種星形多面體。 它的外形是一個Ef₁g₁星狀的二十面體。 溫尼爾在他的書中列出28種星形多面體模型，並將凹五角錐十二面體列為第三個星狀的二十面體。

凹五角錐十二面體
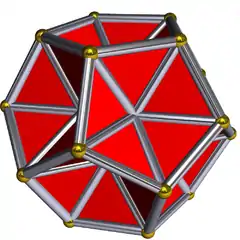(點選檢視旋轉模型)
類別	星形多面體
面	20
邊	60
頂點	20
歐拉特徵數	F=20, E=60, V=20 (χ=-20)
面的種類	星形六邊形
頂點圖	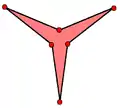凹六邊形
對稱群	二十面體群 (Ih)
參考索引	W28, 26/59
對偶	自身對偶
星狀圖 星狀核 凸包 二十面體 十二面體

性質

頂點坐標

凹五角錐十二面體的凸包是正十二面體，因此其頂點坐標與正十二面體相同：

(±1, ±1, ±1)

(0, ±1ϕ, ±ϕ)

(±1ϕ, ±ϕ, 0)

(±ϕ, 0, ±1ϕ)

其中ϕ = 1 + √52為黃金比例。

作為星形多面體

凹五角錐十二面體作為星形多面體時，其面為一種星形六邊形。整個立體共有20個面、60條邊和20個頂點[1]。

星狀圖	星形	星狀核	凸包
		正二十面體	正十二面體

作為凹多面體

凹五角錐十二面體作為凹多面體時，與五角化十二面體和小星形十二面體有相同的拓樸結構，都是用五角錐取代正十二面體的五邊形面，其差別在於，五角錐的高度，接至外接球的是五角化十二面體，高度更高的是小星形十二面體，高度為負的就是凹五角錐十二面體。

• 
  小星形十二面體
• 
  五角化十二面體
• 
  正十二面體
• 
  倒五角化十二面體
  凹五角錐十二面體

作為刻面的多面體

在幾何學中，刻面是一種移除多面體的某些部份卻不產生新的頂點的一個動作。凹五角錐十二面體與將正十二面體經過構建20個自我相交的六邊形面的刻面所形成的形狀有相同的形式。這種形式是一種諾貝爾多面體。

其凸包的20個頂點的頂點布局與正十二面體的頂點布局相同。

• 
  將星形的凹五角錐十二面體中的其中一個六角星面反白顯示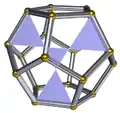
• 
  這些面可以看做是從正十二面體刻面而來

相關多面體

• 
  與凹五角錐十二面體與五角化十二面體有著類似的結構，其差別僅在一個是正十二面體向外接錐體另外個是減去錐體

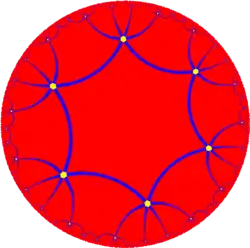
凹五角錐十二面體在拓樸中相當於六階六邊形鑲嵌的商空間，其可以將作為星形多面體的凹五角錐十二面體中的六角星面進行拓樸變形成正六邊形而構造出六階六邊形鑲嵌，因此在另外一個索引中也被看作是一種正多面體[2]：

實心凹五角錐十二面體

布里居在1974年描述了一個外型與凹五角錐十二面體相似的多面體。布里居發現凹五角錐十二面體中央的部分因為重疊所以不算是凹五角錐十二面體的一部份，因而導致凹五角錐十二面體中心密度是0，因此其描述了一個有中間部分的凹五角錐十二面體[3][4]。

	凹五角錐十二面體	布里居的實心凹五角錐十二面體
星狀圖

複合大三角六邊形二十面體凹五角錐十二面體

複合大三角六邊形二十面體凹五角錐十二面體是指由大三角六邊形二十面體和凹五角錐十二面體重疊組合成的一種幾何形狀。

其也是一種星形二十面體。

星狀圖	星形	星狀核	凸包
		正二十面體	正二十面體

參考文獻

1. . dmccooey.com. [2018-08-25]. （原始内容存档于2016-08-07）.
2. The Regular Polyhedra (of index two) 页面存档备份，存于, David A. Richter
3. Guy's polyhedra pages. . steelpillow. 2006-07-11 [2016-08-31]. （原始内容存档于2016-03-13）. Precursor: FmFq, Du Val symbol: Ef₁g₁
4. G. Inchbald, In search of the lost icosahedra, Math. Gaz. 86 (July 2002) pp. 208-215.