斜方二十面體

在幾何學中，斜方二十面體是一中星形均勻多面體，由30個正方形和20個正六邊形組成，是一種無法直接由施萊夫利符號或考克斯特記號表示的均勻多面體。 [1]

斜方二十面體
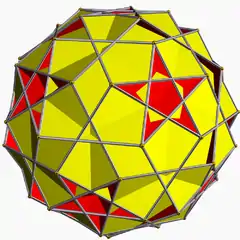斜方二十面體
類別	星形均勻多面體
面	50
邊	120
頂點	60
歐拉特徵數	F=50, E=120, V=60 (χ=-10)
面的種類	30個正方形 20個正六邊形
面的佈局	30{4}+20{6}
頂點圖	4.6.^4/3.^6/5
威佐夫符號
對稱群	Ih, [5,3], *532
參考索引	U56, C72, W96
對偶	變數 "對偶多面體" 未定義。
特性	頂點正、非凸
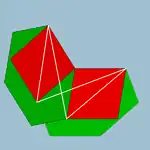4.6.^4/3.^6/5 （頂點圖）
變數 "對偶多面體" 未定義。 (對偶多面體)

性質

斜方二十面體的外觀與斜方截半大十二面體移除正五邊形和正五角星（或稱正5/2角形[2]）的結果十分類似[3]。實際上要從斜方截半大十二面體透過移除正五邊形和正五角星面構成一個斜方二十面體還需要在當中適當的位置補上正六邊形面才能構成，而當中的正方形面則為斜方截半大十二面體與斜方二十面體共同擁有的部分[4]。

斜方二十面體

斜方截半大十二面體

面的組成

外觀上，斜方二十面體由30個正方形和20個正六邊形組成，但考慮到其拓樸結構，如面連接的方向，則斜方二十面體可視為由4種多邊形組成，分別為正方形，施萊夫利符號{4}、正六邊形，施萊夫利符號{6}、反著連接的正方形，施萊夫利符號{4/3}以及反著連接的正六邊形，施萊夫利符號{6/5}，其數量分別為正方形15個、反著連接的正方形15個、正六邊形10個以及反著連接的正六邊形10個[5]。其面在頂點周圍的分布為：每個頂點都是正方形、正六邊形、反著連接的正方形和反著連接的正六邊形的公共頂點，在頂點圖中可以用{6, 4, 6/5, 4/3}表示[6]。

面在頂點周圍的分布

相關多面體

有數種均勻多面體與均勻多面體複合體和斜方截半大十二面體共用頂點排佈，分別為十複合三角柱、二十複合三角柱和斜方截半大十二面體等。

凸包	斜方截半大十二面體
斜方二十面体	十複合三角柱	二十複合三角柱

全截大二十面體

全截大二十面體
全截大二十面體
類別	退化星形均勻多面體
面	62
邊	120
頂點	60
歐拉特徵數	F=62, E=120, V=60 (χ=2)
面的種類	12個退化截角五角星 20個正六邊形 30個正方形
頂點圖	2[4,6,10/2]
考克斯特符號
施萊夫利符號	t0,1,2{^5/2,3}
對稱群	Ih, [5,3], *532
特性	頂點正、非凸
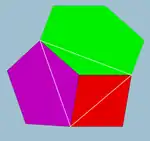2[4,6,10/2] （頂點圖）

全截大二十面體是一種是一種退化的均勻星形多面體，其外觀與斜方二十面體的12個五邊形空隙中加入退化的截角五角星所形成的立體相同[7]。其中退化的截角五角星為繞兩圈的五邊形，在施萊夫利符號中可以用{10/2}表示[7]。

性質

全截大二十面體為大二十面體經過全截（Omnitruncation）變換的結果。其變換過程與正二十面體變換為大斜方截半二十面体的過程相同，會使原有的面截角，並生成對偶的面截角之結果與正方形面，其通常會與先截半再截角的結果拓樸結構類似或相同[8]。大二十面體經過全截變換後應具有62個面、180條邊和120個頂點，然而因為有部分邊和頂點兩兩重和，[7]因此所形成的立體僅有62個面、120條邊和60個頂點，而此結構正好使歐拉示性數為2。

大截半二十面體

全截大二十面體

斜方二十面體

面的組成

全截大二十面體由12個退化截角五角星、20個正六邊形和30個正方形組成，每個頂點都是重複兩組的正方形、六邊形和退化截角五角星的公共頂點，在頂點圖中可以用2[4,6,10/2]表示[7]。

面在頂點周圍的分布

變種

全截大二十面體有一種變種，即原像施萊夫利符號計為{⁵/₄,3}的全截結果。其結果為斜方二十面體的12個五角星空隙中加入退化的星形十邊形所形成的立體[9]，且該星形十邊形為施萊夫利符號計為{10/4}的星形十邊形，實際上圍繞兩圈的五角星。[9]

參見

• 斜方截半大十二面體

參考文獻

1. Richard Klitzing. . bendwavy.org. [2019-10-14]. （原始内容存档于2018-07-07）.
2. . bbiq.jp. [2019-09-01]. （原始内容 请检查|url=值 (帮助)存档于2019-09-01） （日语）.
3. R. Klitzing. . [2019-10-15]. （原始内容存档于2018-09-17）.
4. George W. Hart. . [2019-10-15]. （原始内容存档于2018-06-23）.
5. {{Cite web |url=http://mathworld.wolfram.com/Rhombicosahedron.html |title=Rhombicosahedron |website=at MathWorld--A Wolfram Web Resource |publisher=Wolfram Research, Inc. |editor-first=Eric W. |editor-last=Weisstein |editor-link=埃里克·韦斯坦因 |accessdate= |quote= |language=en }}
6. . mathconsult. [2019-10-14]. （原始内容存档于2018-05-02）.
7. Richard Klitzing. . bendwavy.org.
8. Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 (pp.145-154 Chapter 8: Truncation, p 210 Expansion)
9. Richard Klitzing. . bendwavy.org.