星形二十面體列表
下表列出了一些可以用二十面體星狀圖表示的星形二十面體,其中有58種收錄於哈羅德·斯科特·麥克唐納·考克斯特的《五十九種二十面體》[1]、21種星形二十面體收錄於《多面體模型》。構成這些星形二十面體的星形胞有12個,分別為a, b , c, d, e1, e2, f1, f1,f2, g1, g2和h。《五十九種二十面體》收錄的多面體中有27種都出現歪斜的外觀。它也包含特殊形狀如大二十面體、複合的多面體、扭曲的形狀,皆只收錄一種。

一種星形二十面體,其杜瓦記號計為De1。
第二種星形二十面體
在幾何學中,第二星狀二十面體是一種非凸多面體,屬於星形多面體,是哈羅德·斯科特·麥克唐納·考克斯特的《五十九種二十面體》中收錄的第二種第二種星形多面體。它可被視為11個多面體的複合體,包括了十個四面體和中間一個大菱形三十面體。它可以被視為多面體的星狀複合物,因此有時稱做複合星狀多面體。該多面體有被溫尼爾的《多面體模型》收錄,其索引為W27。
表格
複合多面體
星形多面體有些可以拆成多個子多面體,換句話說,有些星形多面體是由數個其他多面體組合而成的,較容易理解的類比比如六角星、大衛之星,是由兩個三角形嵌合在一起構成的。下表列出一些由若干多面體嵌合在一起構成的星形二十面體。
| 名稱 | 圖像 | 來源多面體 | 複合數量 | 編號 | 核心是 正二十面體 |
星狀圖 |
|---|---|---|---|---|---|---|
| 五複合正四面體 |  |
正四面體 | 5 | 47 (59) | 是 | 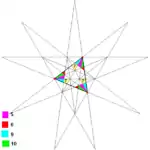 |
| 十複合正四面體 |  |
正四面體 | 10 | 22 (59) W25 |
是 | 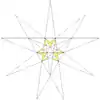 |
| 五複合正八面體 小星形十二面體 |
 |
正八面體 | 5 | W51 | 否 截半二十面體 |
 |
| 小星形十二面體 | 1 | |||||
| 六複合五方偏方面體 |  |
五方偏方面體 | 6 | 4 (59) | 是 |  |
| 五複合正八面體 |  |
正八面體 | 5 | 是 | 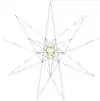 |
星形二十面體
下列表格以杜瓦記號開頭字母分類。
- A
| 杜瓦記號 | 圖像 | 編號 | 名稱 | 說明 | 星狀圖 |
|---|---|---|---|---|---|
| A |  |
1 (59) W4 |
正二十面體本身 |  | |
| Af2 | |||||
| Af2g1 | |||||
| Af2g2 | |||||
| acdf2g1 |  |
- B
| 杜瓦記號 | 圖像 | 編號 | 名稱 | 說明 | 星狀圖 |
|---|---|---|---|---|---|
| B |  |
2 (59) W26 |
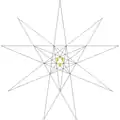 | ||
| Be1 | |||||
| be2 |
- C
| 杜瓦記號 | 圖像 | 編號 | 名稱 | 說明 | 星狀圖 |
|---|---|---|---|---|---|
| C |  |
3 (59) W23 |
五複合正八面體 |  | |
| Ce2 | |||||
| Cf2g1 |  |
- D
| 杜瓦記號 | 圖像 | 編號 | 名稱 | 說明 | 星狀圖 |
|---|---|---|---|---|---|
| D |  |
4 (59) | 六複合五方偏方面體 | 6個五方偏方面體的複合體(頂角藏在裡面) |  |
| De1 |  |
21 (59) W32 |
 | ||
| De1f1 |  |
24 (59) | |||
| De1f1d |  |
35 (59) | |||
| De1f1g1 |  |
25 (59) | |||
| De1f1df2 | |||||
| De1f1df2g1 | |||||
| De1f1df2g2 |  |
44 (59) | |||
| De1f1dg1 |  |
38 (59) | |||
| De1f1dg2 |  |
41 (59) | |||
| De1g1 | |||||
| De2 |  |
27 (59) | |||
| De2f1d |  |
46 (59) | |||
| De2f1df2g1 |  |
55 (59) | |||
| De2f1df2g2 |  |
58 (59) | |||
| De2f1dg1 |  |
49 (59) | |||
| De2f1f2 |  |
52 (59) | |||
| De2f2 |  |
30 (59) W34 |
大三角六邊形二十面體 |  | |
| De2f2_ |  |
內側三角六邊形二十面體 |  | ||
| De2f2g2 |  |
31 (59) | |||
| Df1 | |||||
| Df2 |
- E
| 杜瓦記號 | 圖像 | 編號 | 名稱 | 說明 | 星狀圖 |
|---|---|---|---|---|---|
| E |  |
5 (59) | |||
| Ef1 |  |
22 (59) W25 |
十複合正四面體 |  | |
| Ef1d | 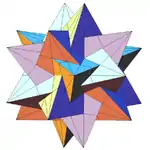 |
47 (59) W24 |
五複合正四面體 |  | |
| Ef1df2 |  |
53 (59) | |||
| Ef1df2g1 |  |
56 (59) | |||
| Ef1df2g2 |  |
59 (59) | |||
| Ef1dg1 |  |
50 (59) | |||
| Ef1g1 |  |
26 (59) W28 |
凹五角錐十二面體 | 看起來像凹十二面體 | 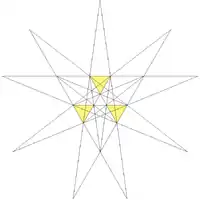 |
| Ef1g1_ | 實心凹五角錐十二面體 | 外觀同於凹五角錐十二面體,但中心不是空的 |  | ||
| Ef2 |  |
28 (59) |  | ||
| Ef2g2 |  |
32 (59) | |||
| e1 |  |
9 (59) W37 |
 | ||
| e1f1 |  |
12 (59) | |||
| e1f1d |  |
34 (59) W36 |
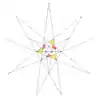 | ||
| e1f1df2g2 |  |
43 (59) | |||
| e1f1dg1 |  |
37 (59) W39 |
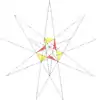 | ||
| e1f1dg2 |  |
40 (59) | |||
| e1f1g1 |  |
13 (59) | |||
| e1g1 |  | ||||
| e2 |  |
15 (59) | |||
| e2f1 |  |
45 (59) W40 |
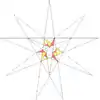 | ||
| e2f1df2 |  |
51 (59) W38 |
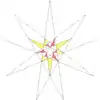 | ||
| e2f1df2g1 |  |
54 (59) | |||
| e2f1df2g2 |  |
57 (59) | |||
| e2f1dg1 |  |
48 (59) | |||
| e2f2 |  |
18 (59) | |||
| e2f2g2 |  |
19 (59) |
- F
| 杜瓦記號 | 圖像 | 編號 | 名稱 | 說明 | 星狀圖 |
|---|---|---|---|---|---|
| F |  |
6 (59) W27 |
Ef1與De2f2的複合體 |  | |
| Fg1 |  |
23 (59) W31 |
內側三角六邊形二十面體(De2f2)與凹五角錐十二面體(Ef1g1)的複合多面體 | 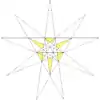 | |
| Fg2 |  |
29 (59) W33 |
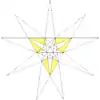 | ||
| f1 |  |
10 (59) | |||
| f1d |  |
33 (59) W35 |
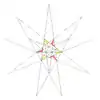 | ||
| f1df2g2 |  |
42 (59) | |||
| f1dg1 |  |
36 (59) | |||
| f1dg2 |  |
39 (59) | |||
| f1g1 |  |
14 (59) | |||
| f2 |  |
16 (59) | |||
| f2g2 |  |
20 (59) W30 |
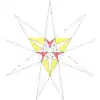 |
- G
| 杜瓦記號 | 圖像 | 編號 | 名稱 | 說明 | 星狀圖 |
|---|---|---|---|---|---|
| G |  |
7 (59) W41 |
大二十面體 |  | |
| g1 |  |
11 (59) W29 |
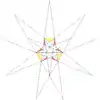 | ||
| g2 |  |
17 (59) |
- H
| 杜瓦記號 | 圖像 | 編號 | 名稱 | 說明 | 星狀圖 |
|---|---|---|---|---|---|
| H |  |
8 (59) W42 |
完全星形二十面體 | 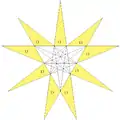 | |
| Hj2 | 五複合立方半無窮 星形菱形十二面體 |
其對偶多面體為 五複合立方半菱形十二面體 或稱五複合刻面半立方體 (compounds of five hemi facetted cube) |
 |
參見
參考文獻
- H·S·M·考克斯特. . H. T. Flather, J. F. Petrie. Springer Science & Business Media. 2012. ISBN 9781461382164.
- . Virtual Polyhedra, George W. Hart. 1996.
- Roman E. Maeder. . mathconsult.ch. 1998.
- Guy's polyhedra pages. . steelpillow. 2006年7月11日 [2016年3月18日]. (原始内容存档于2016年3月13日).
外部連結
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.